《图灵完备》游戏攻略第一章:基础逻辑电路
-
《图灵完备 Turing Complete》游戏攻略保姆级详解。
第一章:基础逻辑电路
前言
我们进入了第一章:基础逻辑电路。在这一章中,我们会搭建出所有常用的逻辑门。
原力觉醒
关卡解析
在这关中我们学会了连接导线,把输入与输出连接在一起即可。
本关最终答案
与非门(NAND)
关卡解析
这关的问题是“电路中的与非门有什么效果”,其实就是要让我们探索与非门的性质。
我们先了解什么是真值表,它由输入和输出构成,它展示的是当电路的输入是什么,对应的输出是什么。
我们只需要开关左上角的输入,查看输出的结果,填写真值表,即可。比如我们先把两个都调为红色,发现结果是绿色,则在输出里的第一列填写绿色。
边测试边填写,理解与非门的原理,理解真值表是什么,填写完后即可过关。
本关最终答案
与非门(NAND)
这关中我们理解了与非门,与非门是逻辑门的一种,它是电路元件中最基础的两个部分之一。通过上面的试验,我们知道了与非门的性质。请确保你理解了它的性质。
与非门的性质:两端输入均为绿,则输出红,否则输出绿。
非门(NOT)
关卡解析
这关要我们构造一个非门。通过观察下方真值表,我们可以看出:非门就是把输入结果取反,然后再输出。输入红就输出绿,输入绿就输出红。

我们使用上一关的与非门,如此连接。
本关最终答案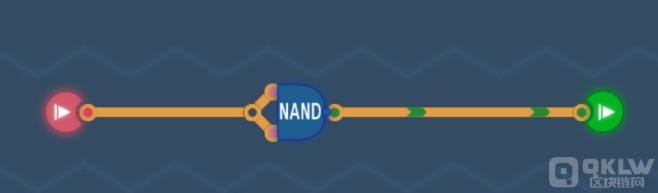
我们可以看到,当输入端输入绿色,与非门的两端就都是绿色。根据与非门的性质“当两路输入均为绿色则输出红色”,也就做到了反转。那么如果输入端输出的是红色,与非门的两端就都是红色。根据与非门的性质“其余情况全部输出绿色”,此时输出的就会是绿色,也做到了反转。
非门(N)
这关我们搭建的整个电路,放在一起,叫做“非门”,这是我们学习的第二个逻辑门。
非门的性质:将输入的结果取反。
与门(AND)
关卡解析
这关要我们构造一个与门。通过观察下方真值表,我们可以看出与门的性质:当两端输入都是绿,就输出绿(其余情况都输出红)。
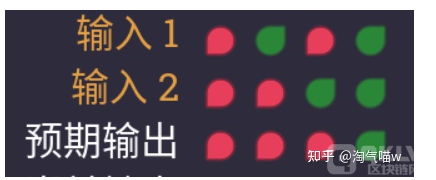
我们如此搭建:
与非门(NAND)的性质我们已经讲过两次:两端都是绿,输出红。
我们再来看一下与门的性质:两端都是绿,输出绿。
我们可以发现,与非门和与门在判断条件上是一样的,而输出的结果刚好相反。我们可以看一下上方真值表,其实“预期输出”和“当前输出”也是刚好相反。那么我们就可以在电路上加一个非门,将结果反转。
本关最终答案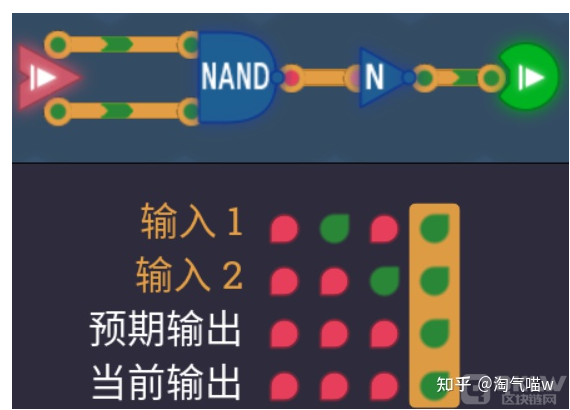
与门(AND)
这关我的搭建的整个电路,放在一起,叫做“与门”,这是我们学习的第三个逻辑门。
与门的性质:两端输入都是绿,则输出绿,否则输出红。
名称构成
我们已经学习了与门和与非门,我们发现它门之间其实只差一个字。其实 与非门 就是在 与门 的基础上再加一个 非门 ,可以简单理解为 与门+非门=与非门。
在这关中,我们应用的是 与非门+非门=与门,两个非“抵消了”。
通过这一点我们可以学习某些逻辑门名称的构成方式,其实这些名称很浅显易懂,之后有些逻辑门也是使用这种方法命名。
或门(OR)
关卡解析
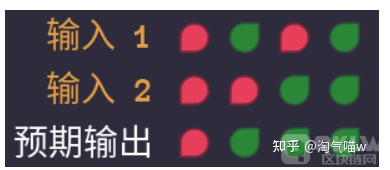
这关的要求是做一个或门。观察上方真值表,我们可以得知或门的性质:只要有一个绿,就输出绿。
本关最终答案
我们在与非门的基础上,使用非门将输入反转,就会得到或门。这是为什么呢?
德·摩根定律
我来用通俗的语言来解释一下这个定律:
如果对输入取反(也就是在电路左侧加非门),结果就会左右对称。
如果对输出取反(也就是在电路右侧加非门),每个结果会分别取反。
来举个例子,我们在上面将与非门的左侧加上非门,根据德·摩根定律的第一条,即对输入取反,我们观察NAND和OR的真值表,可以发现它们的输出确实是左右翻转的对称关系。我们在这关中能从与非门(NAND)获得或门(OR),正是应用了德·摩根定律。
请确保你理解了德·摩根定律。
或门(OR)
在这一关中我们获得了或门。
或门的性质:只要有一个为绿,就输出绿。
基础逻辑
我们学习过了 与、或、非 这三个逻辑门,它们是最常用最重要的逻辑门。让我们来复习一下:
与门:都是绿,输出绿。
或门:只要有一个为绿,输出绿。
非门:对输入取反。
或非门(NOR)
关卡解析
如果你还没有学习过德·摩根定律,请先学习(在目录里查看)。
让我们再次请出德·摩根,帮助我们分析。

这关我们的材料有与非门(NAND)和非门(N),我们需要得到的是或非门(NOR),我们观察德·摩根定律,发现NAND和NOR是对角的关系(NAND在左下角,NOR在右上角)。那么我们如果想要从NAND获得NOR,其实就简单了,只需要“既对输入取反,又对输出取反”,即在电路的两侧都加上非门。
本关最终答案
或非门(NOR)
或非门的性质:两个都是红,就是绿。
我们已经学习过了 与非门(NAND) 和 或非门(NOR),在现实的电路中,这两个逻辑门是电路中最基础的组成部分。
如果你只是想要玩这个游戏,目前为止你并不需要去刻意的记住 与、或、非 三个逻辑门之外的其他逻辑门的性质,只需要理解。以后多使用,熟悉,用的时候再查看即可。
高电平
关卡解析
这关要求我们制造一个不管怎样都输出绿色的电路。我认为应该有多种解决方式,这是我的方法:
本关最终答案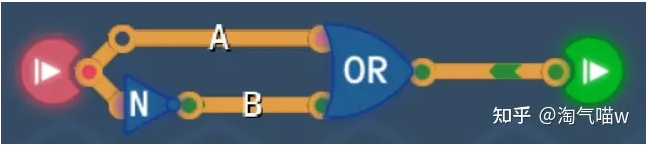
两条路,A没有非门,B有非门。这样,当输入是绿色,A就是绿色,当时如是红色,B就是绿色,保证了总有一条路是绿色的。在后面加入一个或门,根据或门的性质,只要有一个是绿,就是绿,就可以保证结果一定是绿。
高低电平
高电平(ON)会作为电子元件加入我们的背包,它是我们接触的第一个没有输入端只有输出端的元件,也就是说它不需要接收任何数据,它不管怎样都会一直输出绿色。
于此同时,低电平(OFF)也会加入,它也没有输入端,不管怎样都会一直输出红色。

第二刻
关卡解析
这关主要是教会我们一种新的思路,反向思考问题。要求我们只在第二刻输出绿。

我们观察第二刻,发现这道题其实是这样的:“只有当输入1是绿,且输入2是红时,输出绿,否则输出红。”据此,我做出了这样的电路:
本关最终答案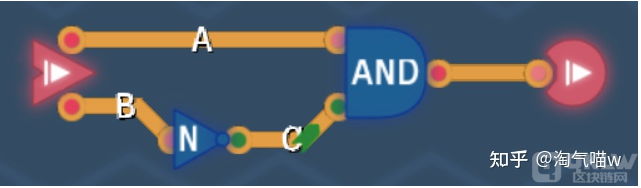
其实这里的思路有点像编程里的判断:
- if A==True and B==False:
- return(True)
- else:
- return(False)
我们学习了一种新的思路,即从输出向输入推理,先设定“判断方式”,再设定“条件”。
异或门(XOR)
关卡解析
这关的难度有所提高,要求我们制造出异或门(XOR),我们观察真值表:

结合真值表和“异或门”这个名字,我们可以得知异或门的性质:如果两个输入不一样,就输出绿色。这也就是为什么名字里有“异”这个字。我们来思考一下,如果想让两个输入不一样,那么就至少得有一个绿色,所以我们先用或门来进行判断是否至少有一个是绿色。
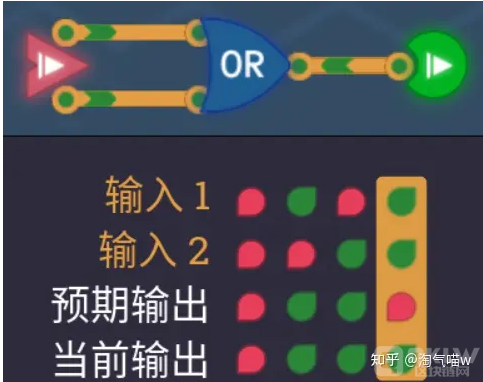
我们发现只有第四刻是错误的,我们需要排除两个都是绿这种情况。我们在输出2上增加一条支路,在上面加入了一个非门,并且对此结果和或门产生的结果进行一个与门判断,就变成了“输入1和输入2至少一个为绿,并且输入2不是绿时,输出绿”。
在这种情况下运行,我们发现第四刻被修复了,但是第三刻又出了问题。“输入1和输入2至少一个为绿,并且输入2不是绿时,输出绿”其实是不全面的,我们还需要一个逻辑:“输入1和输入2至少一个为绿,并且输入1不是绿时,输出也是绿”,这样才能确保第三刻的情况也被考虑到。
到这里,我认为此题其实有不止一种解题方式,但是我只找到一种——将电路翻一倍。
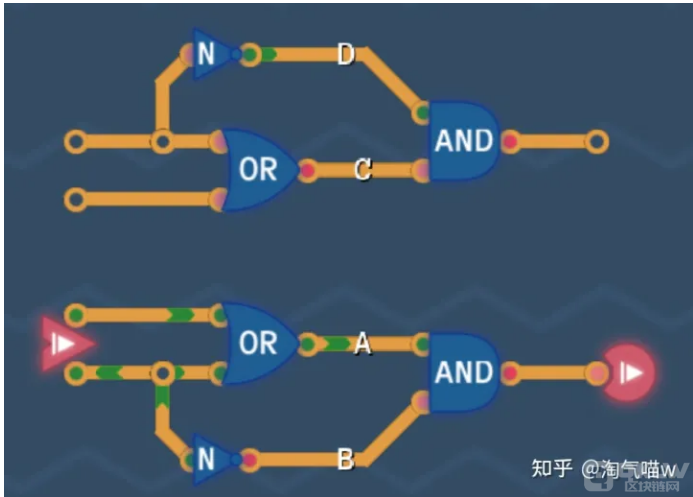
我们把原来的电路上下翻转一下,得到一个新的电路,此电路可以判断“输入1和输入2至少一个为绿,并且输入1不是绿时,输出也是绿”,然后我们将两个电路合起来,再用一个或门连接:
本关最终答案
这就是我们这关最终的电路,也就是异或门。
异或门(XOR)
异或门的性质:当输入不同,输出绿。
三路或门
关卡解析
接下来的两关比较简单,三路或门,顾名思义就是有三个输入端的或门。它的性质和或门是一样的:“只要有一个是绿,就输出绿”
我们先判断其中两个是否有绿色,获得的结果再和第三个判断是否有绿色,即可。
本关最终答案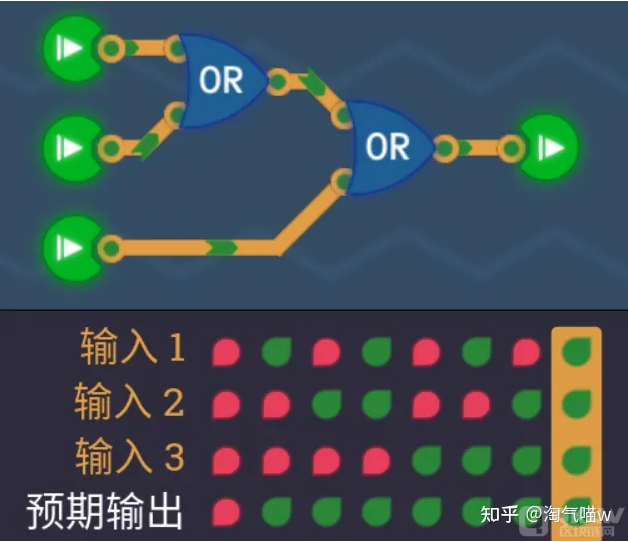
三路与门
关卡解析
三路与门,顾名思义就是有三个输入端的与门。它的性质和与门类似:“三个都是绿,就输出绿”。其实我们只要把上一关的或门换成与门即可。先判断输入1和输入2,判断的结果在和输入3做判断。
本关最终答案
同或门(XNOR)
这是我们 第一章:基础逻辑电路 的最后一关。
关卡解析
这关的关卡目标给了我们很明显的提示,“搭建一个和异或门输出相反的逻辑门,即同或门(XNOR)”,这意味着我们可以完完全全从逻辑门的名字出发。“异或门”和“同或门”这两个词语唯一和差别是“异”和“同”,我们只需要将异或门加上一个非门即可将“异”变为“同”。
其实本关也可以从另一个思考角度出发,即德·摩根定律。如果想把输出结果取反,需要在电路的右侧加非门。
本关最终答案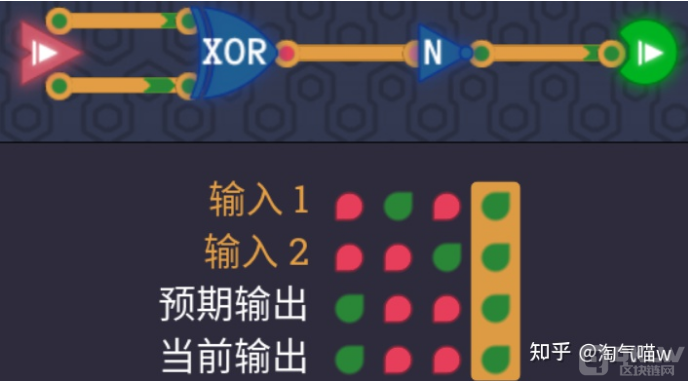
同或门
同或门的性质:输入不一样,就输出红。
《图灵完备 Turing Complete》游戏攻略保姆级详解
你可以通过《图灵完备》这款游戏,学习处理器架构,搭建自己的伟大作品。游戏闯关模式的最终目标是搭建一台可以运行的计算机。我将会开始更新这款游戏的攻略,详细解析每一关的通关思路,并且讲解背后的原理。
以下三章为《图灵完备 Turing Complete》游戏手把手教程(教程原创为知乎:淘气喵w,特此说明)
第一章:基础逻辑电路
第二章:算术运算和存储器
第三章:处理器架构




 2387813
2387813 







